I love applying math in a practical way. Here is a script I created that triangulates the coordinates of a target point based on three reference points and then outputs another target point based on a new set of reference points. An example of when this could be useful is for saving poses on a joint based face rig. If you set up poses on one face you could potentially apply them to other faces of different proportions.
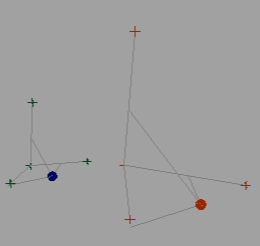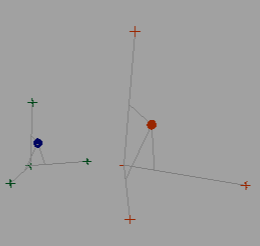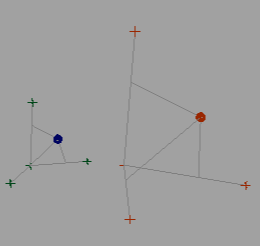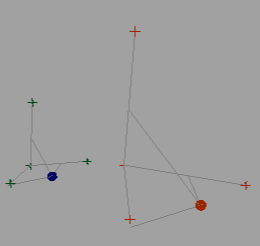
Below is an image of a base space(left side) and a new space(right side). The script triangulates the position of the target (shown as a sphere) in the base space and uses that data to find where the position of the target should be in the new space. The three locators A, B, and C are similar to axis x,y,z, but they can be moved freely around. The script first finds how far along each A,B, and C axis the target is by forming a right angle from the axis to the target. This distance down the axis is the t parameter in the line equation Line = point + t*(Vector). The parameter is then used to find points in the new space’s A, B, and C axis. These points are used to create components in the algorithm. I will refer to these new points simply as point A, B or C. The locators are “reference point†A, B, or C.
There are three components in the algorithm. The A component is a plane equation with a normal of point A – origin. The B component is a ray that is perpendicular to vector formed by point B – origin with a base at point B. The B ray is swept across the A plane creating intersection points. It will stop once it finds a hit. A hit is when the dot product of the vector formed by the intersection point – point C and vector formed by reference point C – point C flips from negative to positive or vice versa.
Its a bit hard to explain, but I’ve included the script and a UI to test it with it!
download it here
in a python tab run:
import dw_triangulate_ui as tui
tui.main()



